Computers, as electronic devices, function at their most basic level as a vast series of electric switches, turning off and on. Each switch state is known as a bit, which is represented as a binary digit, a 1 or a 0. These bits combine into huge collections to represent text, images, files, computer programs, and more. The computer can process these bits in entire streams, but to make them easier for human beings to deal with and understand, they are grouped together.

Firstly, we group them together into “words” or small groups of bits that the computer’s memory can deal with. These have standardized into the byte, which is made up of 8 bits. (There is also use of the term “nibble” or “nybble,” which is half a byte, or 4 bits.) Because it has eight bits, this is specifically referred to as an octet. (There are some places where the term “byte” might refer to six bits or other numbers of bits.)

There are two main systems to group these bytes into larger bundles. The most commonly used system is based on powers of 10, and follows the typical conventions of our denary or decimal number system and the standard system of prefixes (as used in the metric system). In general, CS students should know the terms up to Exabyte.

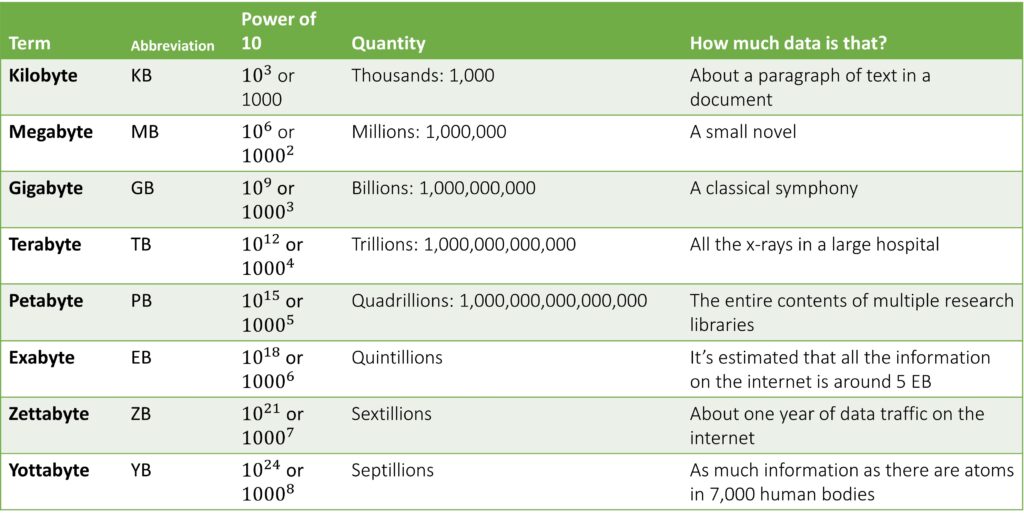
To convert between quantities in this system, you simply multiply or divide by thousands. So, 3MB is 3,000KB or 0.003GB. 2.5TB is 2,500GB or 0.0025PB. As we’re used to the denary system, this is fairly easy – simply appending zeros or moving the decimal point.

The other system is based on the binary system, with powers of 2. These are more technically correct and are the proper terms and quantities for use in computer science. Note that the quantities are very close to the denary groupings, so we can use the standard terms of “millions” or “billions.”

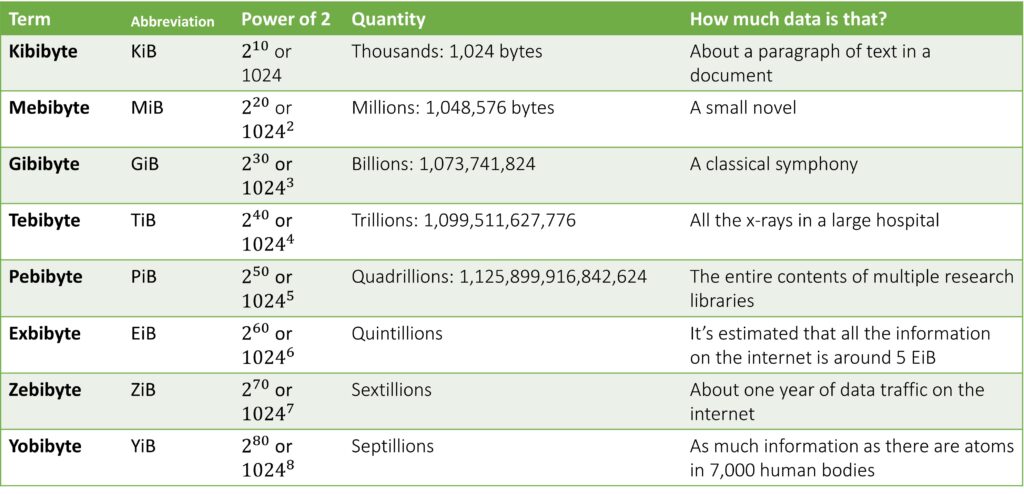
Converting here is not as straightforward, since you need to multiply or divide by 1024. A calculator is really needed. If a student is in an exam situation without a calculator, by remembering that 1024 = 2¹⁰ this can be done more easily by doubling or halving a number ten (or multiples of ten) times. 200,000 bytes can be converted to kibibytes (KiB) by dividing by two (finding half) ten times. Mentally, that’s fairly easy: 100,000 then 50,000 then 25,000 then 12,5000 …and so on until you reach 195KiB (rounded to the nearest KiB). Similarly, you can convert 3.4GiB to MiB by doubling ten times: 6.8 then 13.6 then 27.2 …and so on until you reach 3,481.6 GiB.

There is also a system referred to as the “customary convention” in which these base-2 quantities are referred to using the terms of the previous system. (For example: 1024 bytes would be referred to as a “kilobyte” and not a “kibibyte.”) Many computer hardware vendors use this “customary convention.”

For more information on mebibytes and more, check out my online course “Conquer Computer Science: Data Representation”